To Issue 160
Citation: Vasiev A, “Through Thick and Thin: Modelling the Delivery of Non-Newtonian Formulations”. ONdrugDelivery, Issue 160 (May 2024), pp 48–52.
Alex Vasiev explores the challenges inherent in understanding flow rates in injectable drug delivery when dealing with non-Newtonian fluids, and provides an overview of how to calculate flow rates for power law, Carreau and Cross fluids.
The pharmaceutical industry is currently undergoing a period of rapid innovation, propelled by several factors. These include advancements in the development of biologics, which are becoming increasingly diverse,1 decentralised healthcare practices and a shift towards administering injections less frequently in at-home settings.2 Additionally, small molecules are being designed using artificial intelligence (AI) drug discovery techniques.3 While these therapeutic innovations hold promise, they can also bring forth unforeseen challenges in drug formulation and delivery.
“The modelling of syringeability and delivery of parenteral formulations has often focused on Newtonian models and the Hagen-Poiseuille equation. While this generally performs well, it is not suitable for predicting the behaviour of non-Newtonian fluids.”
These challenges can include ensuring the stability of large or fragile biologics at higher therapeutic concentrations or improving the solubility of poorly soluble APIs. Overcoming these hurdles can require the implementation of sophisticated solutions, such as microcarriers, adjuvants, excipients and stabilising matrices.4 It is crucial to recognise that these formulations profoundly impact the physical properties of drugs and can present challenges for parenteral drug delivery, especially in rapid, automated systems such as autoinjectors.
One example of this is high- concentration monoclonal antibodies, which can experience aggregation under agitation-induced stress. Stabilising matrices composed of polymer, lipid crystal or polysaccharide gels can offer improved stability and efficacy but can exhibit non-Newtonian flow behaviour. This is also true for long-acting injections composed of particulate suspensions where particle particle interactions and alignment can result in the same.
The modelling of syringeability and delivery of parenteral formulations has often focused on Newtonian models and the Hagen-Poiseuille equation. While this generally performs well, it is not suitable for predicting the behaviour of non-Newtonian fluids. This is because non-Newtonian fluids do not uniformly thicken or thin as they pass through a needle; rather, this effect occurs near the needle wall where the fluid experiences the highest shear.
For shear-thinning fluids, this phenomenon results in plug-like flow, which can be seen in the dispensation of fluids such as toothpaste. This results in a very different volumetric flow rate at a given pressure. In autoinjectors, this issue is further complicated by the decay of delivery force over the stroke, which is characteristic of most devices powered by springs or gas.
To tackle this challenge, this article presents an overview of solutions to non-Newtonian fluids described by the power law, Cross and Carreau models. The aim is to provide a toolbox to assist the integration of formulation development and device design. Specifically,it examines model solutions in the context of an autoinjector where the delivery force varies throughout the delivery process. Adopting a standardised approach to predictive modelling can enable the industry to make well-informed decisions early on and provide valuable insights into potential device parameters during formulation development.
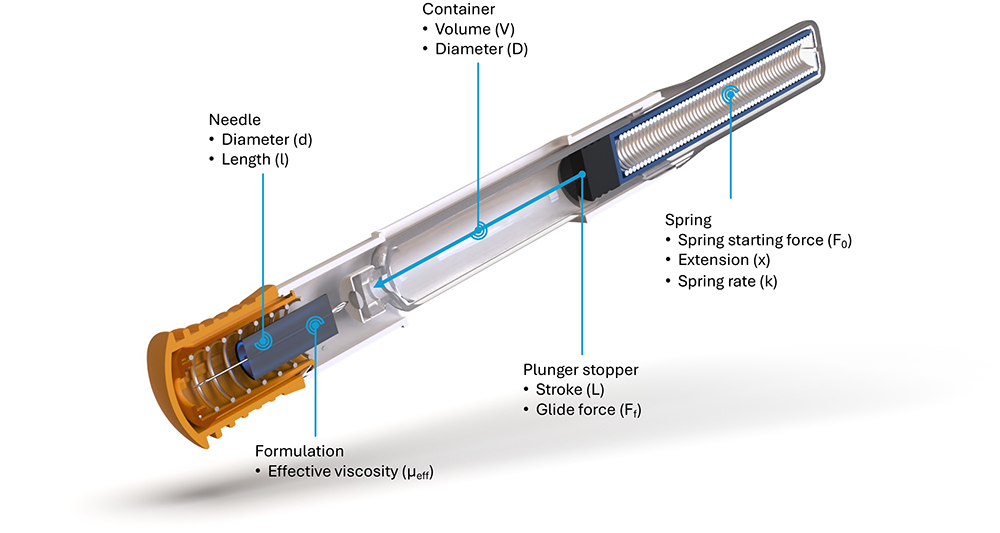
Figure 1: Illustration of autoinjector parameters for the definition of injection time, omitting losses in available force to bubble compression and friction.
DEFINING THE PARAMETERS OF AN AUTOINJECTOR
Consider an autoinjector comprising a primary container with a liquid volume V and an internal diameter D (Figure 1). For illustration,it is assumed that any bubble volume in the container vanishes once the container is pressurised, although this can be accounted for if needed. The liquid occupies a fraction of the container length L equivalent to the delivery stroke:
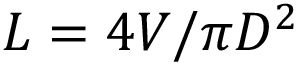
In this example, the work required to deliver the drug is performed by the force of a compression spring, following Hooke’s law, pushing on a rubber plunger stopper within the container:
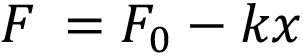
Here, F is the force at a particular instance during delivery, F0 is the force at the start of delivery, k is the spring constant and x represents the spring extension, which, for simplicity, is assumed to correlate to the plunger stopper displacement. The system generates pressure within the container, which, due to the spring constant k, diminishes as delivery progresses. This case is true for most autoinjectors powered by helical compression springs or gas springs. In the event of a system providing constant force, such as an electronic driver or subliming substance, the delivery occurs under a near-steady state.
The force F exerted by the delivery system, after accounting for frictional losses (glide force Ff), creates a pressure P within the container proportional to its cross-sectional area A. This produces a flow rate Q through the needle proportional to the hydrodynamic resistance of the needle (length and diameter), as well as the effective viscosity of the fluid. It is assumed here that no back pressure is present and, therefore, that P within the container is equivalent to ∆P across the needle.
MODELLING NON-NEWTONIAN FLUIDS
The viscosity and shear relationships for non-Newtonian fluids described by the power law, Carreau and Cross fluid models are shown in Table 1.5,6
Defining Volumetric Flow Rate
The local velocity of the liquid in a needle depends on the distance r from the centre axis. Here a definition of volumetric flow rate adapted from a method attributed to Weissenberg, Rabinowitsch, Mooney and Schofield (WRMS)5,6 is used, and combined with definitions for an autoinjector mechanism:
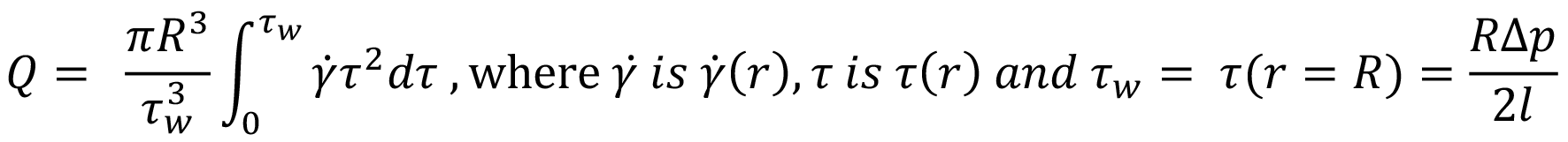
From this, an integral I is derived.6 It is this integral that requires solving to determine the volumetric flow rate for a specific fluid model:
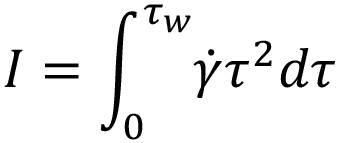
Substituting specific terms for τ and dτ followed by integration provides an analytical solution for a model of interest. In the case of a Newtonian fluid, this results in the familiar Hagen-Poiseuille equation:
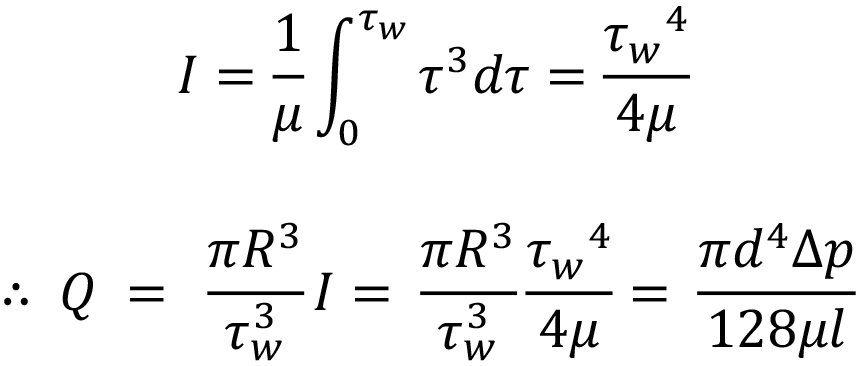
Non-Newtonian Behaviour
It is useful to initially define power law fluid behaviour as it underpins both the Carreau and Cross fluid models. A power law fluid flow profile is not parabolic (plug flow) and affects its volumetric flow rate at a given differential pressure. The magnitude of shear dependency is governed by a flow behaviour index n, while the overall viscosity is regulated by the flow consistency index K. Unlike the Cross and Carreau models, the power law fluid equation for injection time can be analytically solved, as previously reported.7 The normalised transition from parabolic to plug flow, as the value of n decreases, is illustrated in Figure 2.
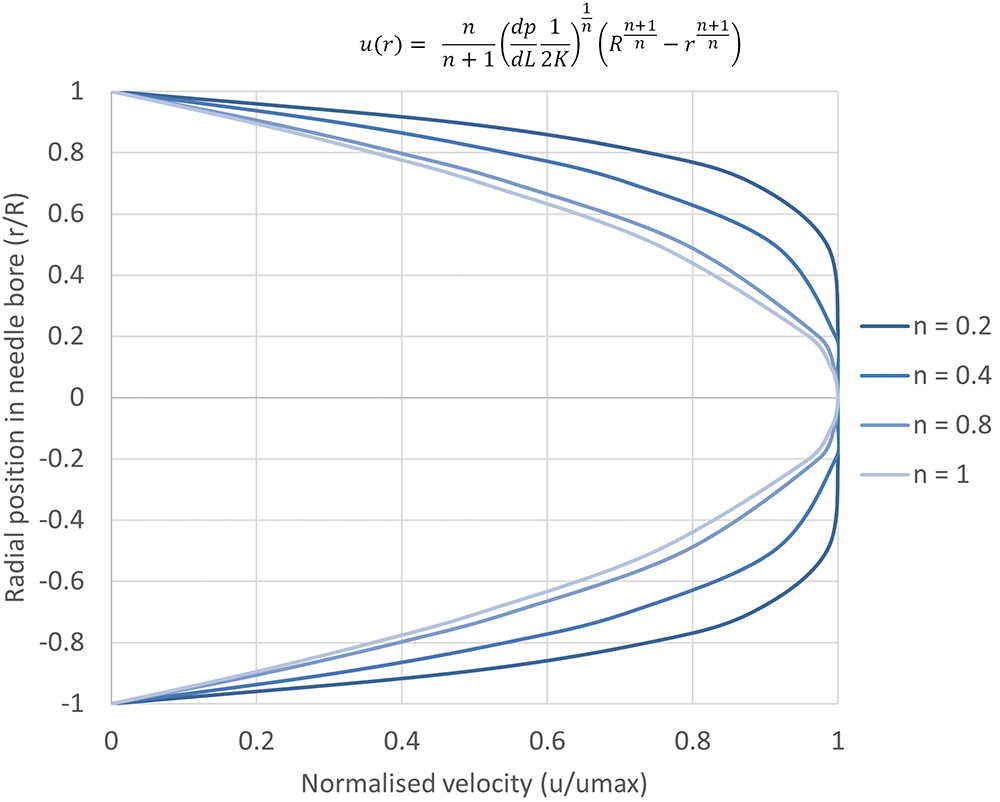
Figure 2: Illustration of the change from a parabolic flow profile to plug flow for a power-law fluid with decreasing flow behaviour index n.
The analytical solution for injection time is found from the definition of the power law fluid volumetric flow rate:
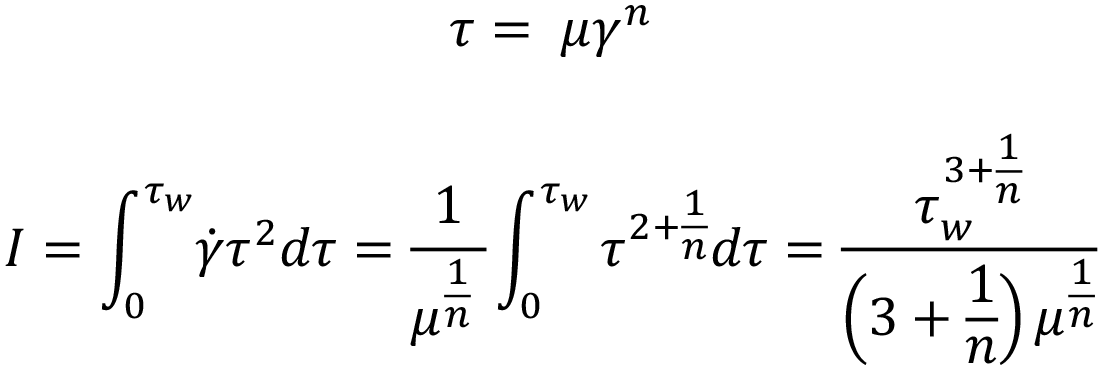
Expanding for I and substituting container diameter D for container radius R gives:
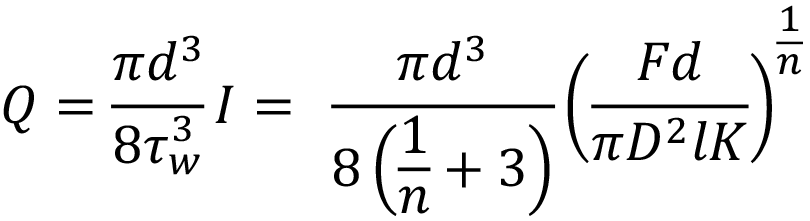
Where F is the applied force, D is the container diameter, d is the needle diameter, l is the needle length, K is the flow consistency index and n is the flow behaviour index. This is combined with the two equations describing the autoinjector to obtain a relation for plunger motion over time7 (note that k for spring index is similar in appearance to K the flow consistency index):
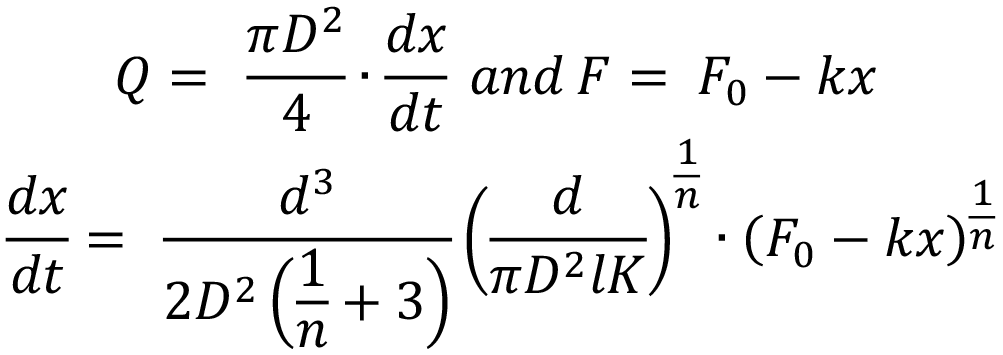
For the purpose of integration, this is simplified by introducing a constant C:

Integration over the stroke results in an analytical solution for injection time for a power law fluid from an autoinjector with a specific needle geometry and spring design:
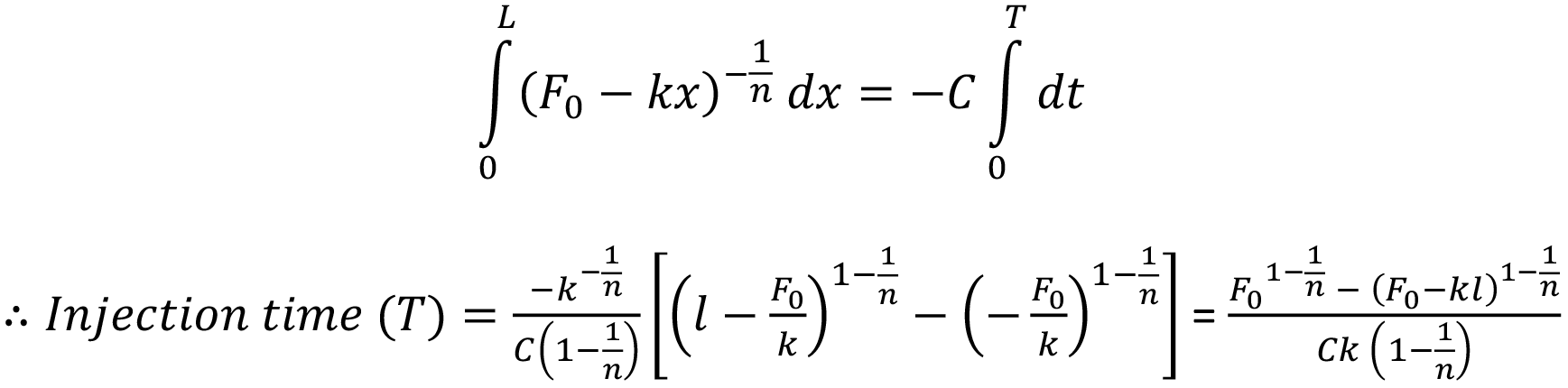
Formulations With Time-Dependent Non-Newtonian Behaviour
Cross and Carreau fluids are more complex, behaving as power law fluids at intermediate rates and Newtonian fluids at both high and low shear rates (Figure 3). They require the definition of four parameters including low- and high-shear viscosities (μ0,μ∞), a characteristic time λ and a flow behaviour index n.
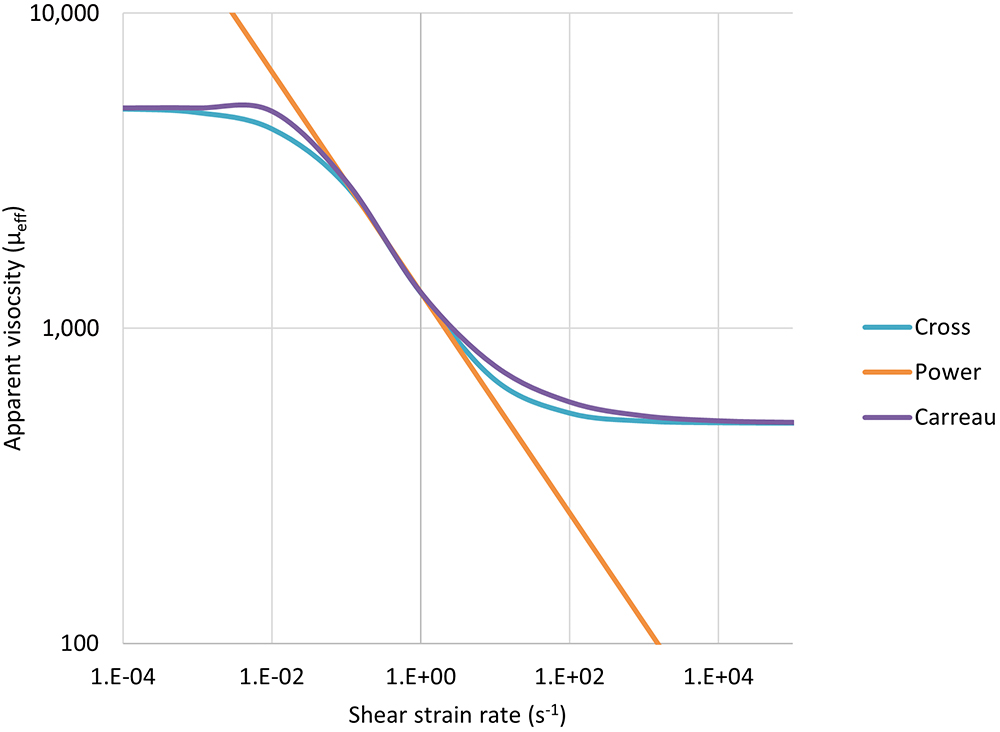
Figure 3: Illustration of the power law, Cross and Carreau apparent viscosity as a function of shear rate.
Finding an analytical solution as the one shown for a power law fluid is not possible because the relationship between flow rate and pressure drop needs to be defined implicitly, requiring a numerical solver. The two solutions start with the same definition from the WRMS method as before,4,5 where:
Carreau Fluid
To solve the integral and calculate volumetric flow rate, the equation defining viscosity for a Carreau fluid is introduced, substituting δ= (μ0–μ∞) and n -1 = n’:
Substituting for τ and dτ into the definition of integral I, changing the integration limits and solving analytically results in a large equation.6
The only thing needed to calculate I is γ ̇w which can be obtained numerically using:
Cross Fluid
The solution of a Cross fluid is similar:
These are substituted into I and solved.6 As with the Carreau model, only γ ̇w is required to do this numerically using the equation:
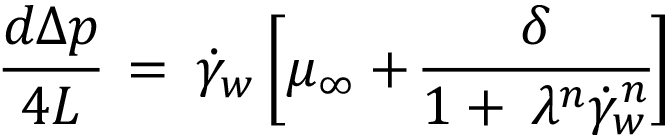
“Understanding the non-Newtonian behaviour of formulations is essential for ensuring the efficacy and safety
of advanced therapies.”
APPLICATION TO AN AUTOINJECTOR PROBLEM
In an autoinjector, Q can be converted to the rate of change of the plunger position over time dx/dt, which correlates to an incremental reduction in available delivery force. The computation of injection time for Cross and Carreau fluids requires an incremental, numerical approach.
Initially the autoinjector system is considered at x = 0 and t = 0. The procedure is to start with the determination of ΔP, γ ̇w,I and, finally, flow rate Q at x(t = 0) = 0 and F(x = 0) = F0. Q is subsequently converted into a change of plunger stopper position over an increment. The new level of force at this spring extension is used to again calculate ΔP, γ ̇w, I and Q. Injection time is the sum of time intervals until the point where x = L, with smaller increments being preferable.
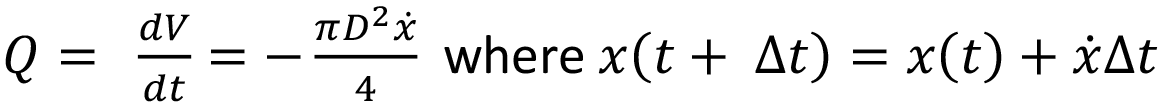
If the autoinjector supplies a constant force, the system can be treated as a steady state over the interval from x = 0 to x = L.
Determination of Constants
The determination of the best fitting model, as well as of the relevant model parameters, is achieved by fitting the models presented in Table 1 to data of the log of the dynamic viscosity against the log of the shear rate. Solvers in programming languages, such as MATLAB or Python, as well as other commercially available rheology software, can be used for this. Before analysing the data, it is important to consider if the experimental conditions cover a sufficiently large span of shear rates. This is to ensure that any Newtonian to non-Newtonian transitions are identified, and that the shear rates are representative of those experienced within an autoinjector.
| Model | Rheological equation | Examples |
| Haggen-Poiseuille | 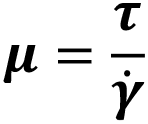 |
Water |
| Power Law | Starch suspension | |
| Cross | 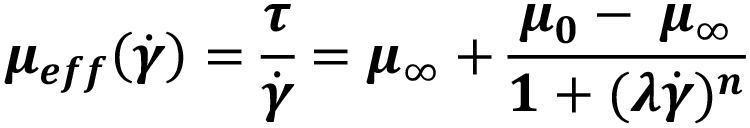 |
Dispersions, polymeric solutions, blood |
| Carreau | 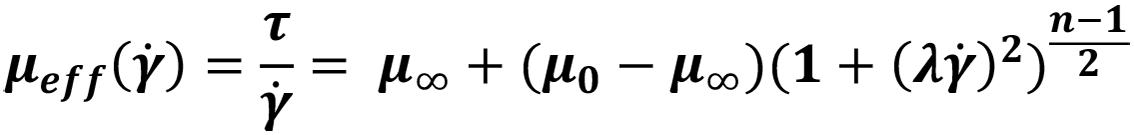 |
Dispersions, polymeric solutions, blood |
Table 1: Definition of common Newtonian and non-Newtonian fluid models with examples.
CONCLUSION
The models provided in this article are a step towards a common toolbox for drug delivery device design and process development. Understanding the non-Newtonian behaviour of formulations is essential for ensuring the efficacy and safety of advanced therapies. By embracing standardised modelling approaches and considering the complexities of non-Newtonian behaviour early in the development process, researchers and developers can de-risk future device development. This becomes more relevant as the industry focuses on established platform devices that may have to deliver increasingly sophisticated formulations in the future.
REFERENCES
- The rise of biologics: Emerging trends and opportunities”. White Paper, CAS, 2023.
- Baryakova TH et al, “Overcoming barriers to patient adherence: the case for developing innovative drug delivery systems”. Nat Rev Drug Discov, 2023, Vol 22(5), pp 387–409.
- Paul D et al, “Artificial intelligence in drug discovery and development”. Drug Discov Today, 2021, Vol 26(1), pp 80–93.
- Jindal AB et al, “Long-acting parenteral drug delivery systems for the treatment of chronic diseases”. Adv Drug Deliv Rev, 2023, Vol 198, Article 114862.
- Skelland AHP, “Non-Newtonian Flow and Heat Transfer”. Wiley, New York, 1966.
- Sochi T, “Analytical solutions for the flow of Carreau and Cross fluids in circular pipes and thin slits”. Rheologica Acta, 2015, Vol 54, pp 745–756.
- Vilaplana M, Vasiev A, White S, “Function-Based Primary Packaging Design for Injecting Viscous Non-Newtonian Formulations”. ONdrugDelivery, Issue 101 (Oct 2019), pp 20–25.

